rangkuman materi matematika kelas 4 semester 2 Kurikulum merdeka bab 5
Bismillah, apa kabar bapak/ibu guru kelas empat jenjang SD/Mi yang kami banggakan. Semoga anda senantiasa dalam keadaan sehat walafiat. Baiklah menjelang pembelajaran ganjil dan genap bulan januari tahun 2022/2023, pada kesempatan baik ini guru-id berbagi rangkuman materi pelajaran matematika kelas IV bab ke lima kurikulum merdeka yang merupakan materi semester 2 (dua) sesuai buku paket kemdikbud terbitan 2022. nah pada kesempatan ini guru-id akan berbagi materi bangun datar sesuai cp 033 , selanjutnya Bagi teman-teman guru yang membutuhkan referensi modul ajar silahkan download melalui tautan di akhir postingan ini.
Materi matematika kelas 4 Kurikulum merdeka Semester 2
Sobat guru matematika jenjang SMA/SMK, sebelum menuju ringkasan materi bab V berikut guru-id bagikan dulu materi dan tujuan pembelajaran (TP) semester 2 sebagai pengingat.
A. Ciri-Ciri Bangun Datar
B. Komposisi dan Dekomposisi Bangun Datar
Tujuan Pembelajaran• menuliskan ciri-ciri segitiga (sama kaki, sama sisi, sembarang, lancip, tumpul dan siku-siku)
• menuliskan ciri-ciri segiempat (jajargenjang, trapesium, layang-layang, belah ketupat, persegi, persegipanjang dan segiempat sembarang)
• menyusun beberapa bangun datar dengan berbagai cara yang mungkin
• mengurai satu bangun datar dengan berbagai cara yang mungkin
Ciri-Ciri Bangun Datar
A. Pengertian Segi Banyak
Banyak benda di sekitar kita yang berbentuk bangun datar. Diantara benda tersebut ada yang termasuk segi banyak dan ada juga yang tidak. Berikut beberapa contohnya:
Untuk memahami jenis dan ciri segi banyak tersebut perhatikan penjelasan berikut:
Jika diperhatikan pada contoh tersebut, dapat diketahui bangun datar tersebut mempunyai sisi berbentuk garis lurus paling sedikit 3 buah dan antarsisi tersebut membentuk sebuah bentuk kurva yang tertutup.
Pada contoh tersebut, diketahui bahwa bangun tersebut mempunyai sisi yang berbentuk garis lurus sebanyak dua buah dan ada juga yang tidak punya sama sekali sedangkan antarsisi membentuk kurva tertutup dan terbuka.
Berdasarkan penjelasan tersebut dapat disebutkan bahwa segi banyak adalah suatu kurva tertutup yang dibatasi paling sedikit tiga buah ruas garis.
A. Jenis Bangun Segi BanyakBerdasarkan besar sudut dan panjang sisinya, bangun segi banyak dibedakan menjadi dua jenis, yaitu :
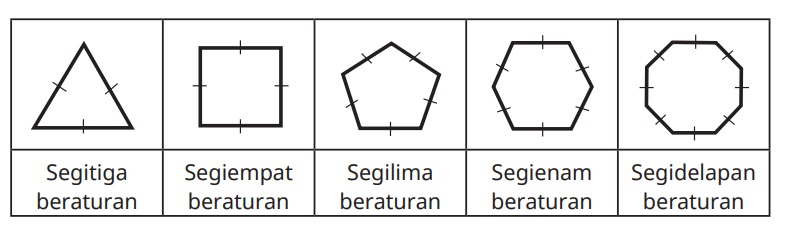
1) Bangun segi banyak beraturanBangun segi banyak beraturan adalah bangun segi banyak yang mempunyai ciri sebagai berikut :
a. Besarnya sudut-sudut dari segi banyak beraturan adalah sama
b. Panjangnya sisi-sisi segi banyak beraturan adalah sama
c. Segi banyak beraturan mempunyai simetri lipat yang sama dengan jumlah sudutnya.
d. Segi banyak beraturan mempunyai simetri putar yang sama dengan jumlah sudutnya.
2) Bangun segi banyak tak beraturanBangun segi banyak tak beraturan adalah bangun segi banyak yang mempunyai ciri sebagai berikut:
a. Besarnya sudut-sudut dari segi banyak beraturan adalah tidak sama
b. Panjangnya sisi-sisi segi banyak beraturan adalah tidak sama
c. Segi banyak tak beraturan mempunyai simetri lipat yang tidak sama dengan jumlah sudutnya.
d. Segi banyak tidak beraturan mempunyai simetri putar yang tidak sama dengan jumlah sudutnya.
Segitiga
Banyak benda di sekitar kita yang berbentuk segitiga seperti penggaris segitiga, rambu lalu lintas dan lain-lain. Bangun segitiga ini memiliki beberapa jenis yang berbeda bentuk dan ciri-cirinya.
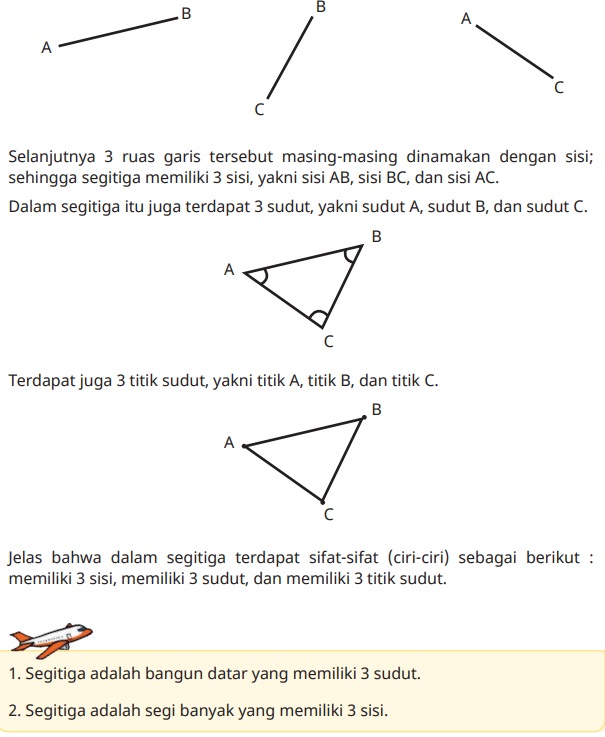
Perhatikan, segitiga di bawah ini. Misalkan nama segitiga tersebut adalah segitiga ABC
Jika kita memperhatikan segitiga di atas, maka kita dapat mengetahui bahwa dalam segitiga terdapat 3 ruas garis yaitu ruas garis AB, BC, dan AC.
Berdasarkan gambar di atas terdapat 3 jenis segitiga, yaitu segitiga sama kaki, segitiga sama sisi, dan segitiga sembarang. Untuk mengetahui sifat-sifat dari ketiga jenis segitiga tersebut perhatikan penjelasan berikut.
Segitiga sembarang adalah segitiga yang sisi-sisinya tidak ada yang sama panjang.
Setelah mempelajari sifat-sifat segitiga berdasarakan sisinya tersebut, dapat dituliskan sebagai berikut :
Segiempat
Perhatikan persegi panjang berikut ini. Misalnya nama persegi panjang tersebut adalah persegi panjang ABCD.
Jika memperhatikan bangun persegi panjang di atas, maka kita dapat mengetahui bahwa dalam persegi panjang memiliki 4 sisi, yakni sisi AB, sisi BC, sisi CD, dan sisi AD.
Dalam persegi panjang itu juga terdapat 4 sudut, yakni sudut A, sudut B, sudut C, dan sudut D.
Terdapat juga 4 titik sudut, yakni titik A, titik B, titik C, dan titik D. Dalam persegi panjang juga terdapat dua pasang sisi yang sejajar, yakni AB// CD dan BC//AD.
Selanjutnya perhatikan semua sudut pada persegi panjang ABCD, terlihat bahwa sudut A, sudut B, sudut C, dan sudut D memiliki ukuran yang sama dan merupakan sudut siku-siku.
d. Belah KetupatPerhatikan belah ketupat berikut. Misalnya nama belah ketupat tersebut adalah belah ketupat ABCD.
Jika diperhatikan bangun datar belah ketupat, maka kita dapat mengetahui bahwa dalam belah ketupat juga memiliki 4 sisi, yakni sisi AB, sisi BC, CD, dan sisi AD.
Dalam belah ketupat itu juga terdapat 4 sudut, yakni sudut A, sudut B, sudut C, dan sudut D.
Terdapat juga 4 titik sudut, yakni titik A, titik B, titik C, dan titik D. Dalam belah ketupat juga terdapat dua pasang sisi yang sejajar sebagaimana yang dimiliki jajargenjang, yakni AB//CD dan BC//AD.
Selanjutnya perhatikan semua sisi pada belah ketupat ABCD, terlihat bahwa sisi-sisi AB, BC, CD, dan AD memiliki panjang yang sama.
Komposisi dan Dekomposisi Bangun Datar
1. Komposisi Bangun Datar
Banyak benda-benda di sekitar kita yang berbentuk gabungan dari bangun datar. Salah satu benda yang sering digunakan oleh kita yaitu permainan tangram. Tangram merupakan permainan yang paling tua yang dikenal dalam matematika, yang sering disebut puzzle china. Tangram merupakan puzzle yang terdiri dari 5 segitiga, 1 persegi dan 1 jajargenjang. Dari tangram ini dapat dibentuk menjadi berbagai macam bentuk yang lain seperti hewan, pohon, orang dan benda lainnya.
Agar kamu paham bagaimana cara mengkomposisi (menggabungkan) berbagai macam bentuk bangun datar menjadi bentuk yang baru, ikutilah prosedur aktivitas berikut ini.
Alat dan Bahan :- Kertas lipat warna-warni
- Gunting dan lem
- Alat tulis
Langkah-langkah :1. Bentuk kelompok yang terdiri dari 3-4 orang.
2. Potonglah kertas lipat warna-warni menggunakan gunting menjadi beberapa bagian dan dinomori seperti dibawah ini.
7. Diskusi bersama anggota kelompok, hal-hal berikut ini.
a. Nama bangun datar apa yang terbentuk?
b. Dapatkah kalian membangun bentuk yang lain dari bangun datar yang sudah ada?
8. Berdasarkan aktivitas yang sudah dilakukan, dapatkah kalian menyimpulkan apakah komposisi bangun datar itu?
LEBIH LENGKAP: